Official Statistics

Sex ratios at birth in the United Kingdom, 2016 to 2020: technical appendices

Published 10 November 2022

Introduction

This report is a supplementary document to the main commentary section of the sex ratios at birth in the United Kingdom publication 2016 to 2020. This document provides technical detail on the methodology and statistical tests used in order to assess whether or not there is evidence for sex selective abortions happening at scale within specific groups in the United Kingdom.

Source data

Ethnicity

Analysis on ethnicity is presented for England and Wales only. This is because the birth registration systems in Scotland and Northern Ireland do not collect data on the ethnicity of the child. We therefore exclude Scotland and Northern Ireland from the birth sex ratio analysis for ethnicity of child.

Ethnicity data is presented by 9 ethnic groups of the babies born in England and Wales, in line with the ethnicity groupings used by the Office for National Statistics (ONS).

Information on ethnicity of the child is routinely collected from mothers as a part of the birth notification data from the NHS Number for Babies (NN4B) system within England and Wales. The ethnicity information included on the birth notification records are linked to the birth registrations; over 99% of birth registration records are successfully linked to their corresponding birth notification record each year.

Birth registration data and country of origin data

Analysis is presented by mother’s country of origin for the United Kingdom.

The ONS provided data for England and Wales for mother’s country of origin and birth order using birth registration data. The registration of births in England and Wales is a service carried out by the Local Registration Service in England and Wales in partnership with the General Register Office.

The National Records of Scotland were used as the source data for Scottish births, by mother’s country of origin, and birth order.

The Northern Ireland Statistics and Research Agency supplied the source data for births, by mother’s country of origin and birth order.

Birth order

The data on birth order relates to the first, second and third or later born children that a woman has had. There is also a category for where the birth order is unknown.

Where birth order data is unknown, these births have been put in this ‘ratio of unknown birth order’ category. From May 2012, imputation of missing data on previous children was discontinued, meaning there are gaps in the data which may not have previously existed while imputation was taking place. Other reasons for the birth order being unknown include this question not being asked at the birth registration and refusal of the mother to answer the question. Missing information on birth order represents a very small proportion of the total births each year (0.3%).

Following advice from the ONS in their 2016 methodological review, unknown birth order has been included as a separate category within this analysis.

Data coverage

Birth registration data for the most recent 5-year time period (2016 to 2020) is aggregated for our analysis to ensure sufficiently large sample sizes are used. The sample reflects the most recent 5-year time period for which finalised data is available.

Even though 5 years’ data has been used in our analysis, the sample sizes for some countries and ethnic groups are still very small. To address this issue, 78 countries with fewer than 100 births in the 5-year period have been excluded.

Calculations and statistical tests

The birth sex ratios were calculated by dividing the number of male births by the number of female births and multiplying this value by 100 to achieve a ratio of the number of males born per 100 females. This calculation was applied to:

• all births in the United Kingdom
• all births, by mother’s country of origin, and birth order, in the United Kingdom
• all births, by ethnicity of child, and birth order, England and Wales

For example, the birth sex ratio for babies born from German mothers over the period 2016 to 2020 was 111 males to 100 females for first born babies and 105 males to 100 females for the second born babies.

Decision on what to compare birth sex ratios against: threshold of 107

This analysis uses an upper value for the natural birth sex ratio of 107. This is based on a review of academic literature,^{[footnote 1] [footnote 2]} advice from academic experts, and an examination of data on birth sex ratios in more developed countries. The aim of this analysis is to investigate if any birth sex ratios are statistically significantly higher than 107, that is, if any group has statistically significantly more than 107 males born for every 100 females, which would indicate sex selective abortions have taken place.

A lower birth sex ratio limit was not used, as we are not investigating whether there are many more females born than males born in the United Kingdom than would be expected.

Testing for birth sex ratios that are statistically significant to the threshold

Birth sex ratios are examined for all births and by birth order (whether a child is first born, second born, third born or more) by the mother’s country of origin and by the child’s ethnicity.

Differences between birth sex ratios and the 107 threshold do occur, but could be due to chance, rather than a real difference. Statistical significance testing is carried out to determine whether any differences observed between the birth sex ratios and the 107 threshold are likely to be ‘real’ or whether they are simply due to chance fluctuations.

This publication uses a number of techniques to test whether ratios over 107 are statistically significant. The first stage of the process is to calculate the probability (‘p values’) that the differences observed could arise by chance as opposed to there being a real difference. We have used the commonly acceptable level of 5% significance level in this analysis, which means that a statistically significant result is found for any p values less than 0.05 (5%) – in other words, such a result would occur rarely by chance alone. However, this methodology presents some difficulties when there are many tests as is discussed below.

The multiple testing problem

The ‘mother’s country of origin’ analysis involved testing the significance level for 177 countries and 5 birth orders, equivalent to 885 statistical tests (although due to missing data 814 tests were carried out as 71 countries in the unknown birth order category had no data available). The ‘ethnicity of child’ analysis involved testing the significance level for 9 ethnic groups and 5 birth orders, equivalent to 45 statistical tests.

When undertaking so many statistical tests, due to random variation it would be expected that some results appear statistically significant due to chance alone. For example, at the 5% significance level used here, you would expect 1 in 20 results to be significant, even if there were no underlying differences from 107. When applied across the 814 and 45 statistical tests carried out here, there is a high chance of incorrect identification of a significant result (a ‘false positive’), leading to inferring evidence about sex selective abortions incorrectly.

To try and solve this issue, also known as the ‘multiple testing problem’, a statistical technique called the Benjamini-Hochberg procedure was applied using the p values already calculated as part of our method to assess statistical significance.

Dealing with the multiple testing problem: Benjamini-Hochberg procedure

In testing whether a result is statistically significant, it is common practice to determine whether the likelihood of an extreme observation occurring by chance is less than 5%. This level of significance is known as the alpha (α) value.

As this analysis involves doing multiple tests for the mother’s country of origin and the ethnicity of the child, this leads to a ‘multiple testing problem’. This is because the probability of getting at least one significant result purely by chance increases with the more tests that are run. The significance level that is set for a single test, α (which measures the probability that a significant result is detected under the assumption that there isn’t one), is not a valid way of detecting a significant result, when multiple tests are being run. To assist in the detection of results which are still significant when many tests are run simultaneously, a correction needs to be made to α. Many approaches have been developed, and for this publication, the Benjamini-Hochberg procedure is used in the analyses presented here.

The Benjamini-Hochberg procedure (B-H step-up procedure) is a way of setting α where it takes into account the fact that there are multiple tests. The procedure is as follows:

• find the significance level (p value) for each individual test
• order the tests in descending order of p values, and give all of the values a rank, called k, with 1 being applied to the biggest p value
• for a given α find the smallest k such that

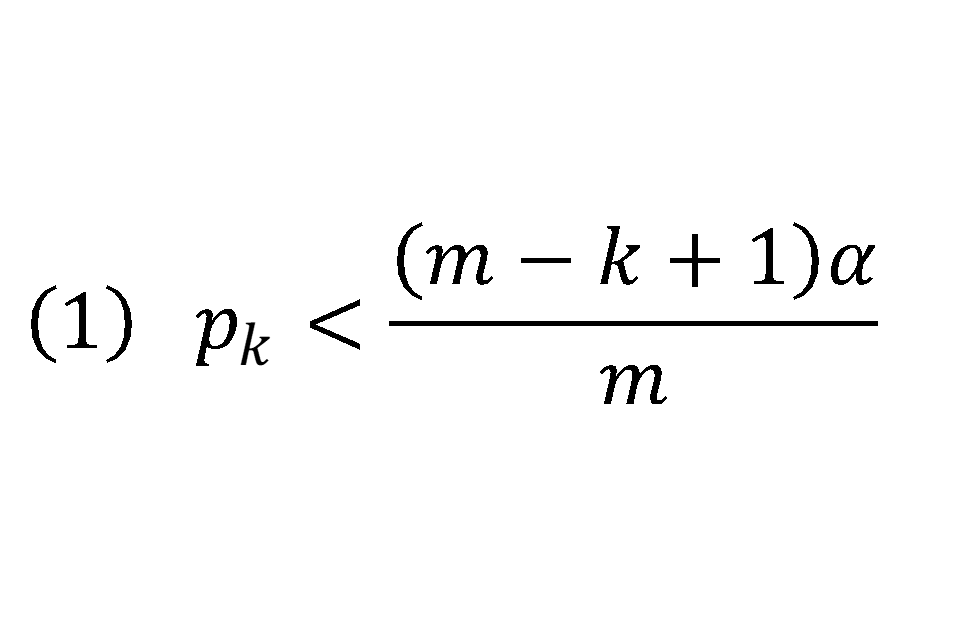
• where m is the total number of tests, then all tests which have a rank of i, where ‘i = k, … , m’ are significant results

A limitation of using this Benjamini-Hochberg procedure is that the groups being tested need to have a large number of births for a relatively small difference in birth sex ratios to be found to lie outside the expected range, and therefore to be identified as being statistically significant. However, the relatively small number of births within many of the groups in this analysis are such that large differences between birth sex ratios and the expected upper limit of 107 would need to be observed for the ratio to be identified as statistically significant. Therefore, evidence would only be identified through this means if sex selection were taking place on a significant scale.

Sensitivity analysis: Storey technique

Given the limitations of the Benjamini-Hochberg procedure, an alternative statistical analysis was conducted to check the validity of the results. Following a review of the methodology in conjunction with the ONS, a supplementary test, known as the Storey technique was recommended and has been implemented since the 2016 publication.

Storey (2002)^{[footnote 3]} and Storey and Tibshirani (2003)^{[footnote 4]} suggested an alternative procedure, where the false discovery rate is estimated for a fixed region called the critical region – that is the range of values under which we would reject the hypothesis of there being no countries or groups with a ratio above 107 – and so the result would be statistically significant. This area is called the q-value and can be compared for different rejection regions as evidence for what proportion of false discoveries is actually seen across the series of tests.

Therefore, the Storey technique is used to estimate how many of the statistical tests performed (814 for ‘mother’s country of origin’ and 45 for ‘ethnicity of child’) were ‘true positives’ at the 5% significance level. This differs from the Benjamini-Hochberg procedure which makes adjustments to the critical values for the group of tests being used, in such a way as to control the false discovery rate (that is, to limit the proportion of outcomes where the test says that a result is significant, but no effect is actually present).

Power considerations

This information on power calculations has been included for illustrative purposes only. Power describes the likelihood of a testing procedure finding a significant result when the underlying sex-ratio is truly in excess of 107.

In testing whether a result is statistically significant, it is common practice to construct the test so that the likelihood of getting a value that is significant, when the true sex ratio does not exceed 107, is less than 5%. This figure of 5% is known as the alpha (α) value. It is also called the ‘size’ of the test, or its ‘significance level’. The power of the test is the likelihood of achieving a significant result when the true ratio is in excess of 107. In simple circumstances the question is how many births do there need to be to be able to construct a 5% significance level test that has a specified power, say 80%, against a specific alternative such as the true ratio being 107.5.

However, the circumstances here are not simple, and we are testing many hypotheses (for example, one for each country and each birth order) simultaneously. It is not possible to evaluate the power of the Benjamini-Hochberg procedure in a straightforward manner.

For illustrative purposes the table below shows how large an observed ratio of males to females would have to be in a single test, before the testing procedure would report a ratio significantly above 107.

For example, to identify a significant result with just 100 births in a single test, the observed sex ratio would need to be at least 149. To identify a significant result in a single test with 100,000 births, the observed sex ratio would need to be 108 or more.

Table 1: required observed sex ratio for the testing procedure to show a result significant at the 5% level for the shown number of births

Number of births	Ratio of males to females x100 in a single test
100	149
500	124
1,000	119
5,000	112
10,000	111
50,000	109
100,000	108

For comparison with the actual data the table below shows how many mothers’ countries of origin had a number of births in the shown range.

Table 2: number of mothers’ countries of origin that were in the shown range of numbers

Number of births	Number of mother’s countries of origin
0 to 99	0
100 to 499	50
500 to 999	28
1,000 to 4,999	53
5,000 to 9,999	14
10,000 to 49,999	24
50,000 to 99,999	3
100,000 to 499,999	4
500,000 or more	1

Previous reports

All previous reports (published each year from 2013) looked at male to female birth sex ratios broken down by the mother’s country of origin. Reports from 2014 onwards also looked at the birth sex ratios by the child’s ethnicity and birth order of the child, in addition to mother’s country of origin.

The 2013 to 2014 and 2016 to 2021 reports showed no statistically significant results in any of the groups analysed.

In the 2015 publication there was one statistically significant result, for Nepalese-born mothers giving birth to their third or later child.

The chances of getting a false positive result (that is, a positive result that is not real) in at least one of a large number of tests is quite high. The statistical technique used to assess whether a result is statistically significant or not (the Benjamini-Hochberg procedure) reduces the chance of these false positive results happening randomly, however it does not completely eliminate it. To further test this result of Nepalese born mothers, another statistical technique (a chi square test), was applied which did not find a statistically significant result, implying the initial result using the Benjamini-Hochberg procedure was likely to be a false positive result.

Following publication of these results in August 2015, an independent review of the methodology was carried out by the Office for National Statistics (see section on Independent review of methodology). This review recommended some changes to the existing Benjamini-Hochberg procedure and the inclusion of an additional statistical technique – the Storey technique. Retrospective application of the modified Benjamini-Hochberg procedure and Storey technique on to the birth sex ratio data analysis published in August 2015 did not find any evidence for a statistically significant group.

Users and uses of birth sex ratio statistics

The birth sex ratio statistics are of interest to the European Council who originally requested their collation. Following the amendment in the Serious Crime Act 2015, Parliament used the statistics within their remit to assess the legality of the Abortion Act and assess the birth sex ratio within the population in Great Britain. Academics and journalists reviewing evidence for sex selective abortions also have an interest in these statistics. Hospital trusts and screening midwives may also have an interest in these statistics when making local decisions for releasing information about the sex of a fetus during routine scans to the public. The United Nations Population Fund review birth sex ratios at a global level.

Independent review of methodology

ONS quality assured the original methodology for this analysis in 2013. In 2016, following continued interest in these statistics, the decision was made to publish birth sex ratios as official statistics. The Department of Health and Social Care (DHSC) asked the Methodology Advisory Service at the ONS to review the methodology and provide assurance that it was a robust approach for reviewing evidence of extreme birth sex ratios.

The recommendations following the independent methodology review led by ONS in April 2016 have all been incorporated into this analysis from the 2016 publication and are presented below:

• when implementing the Benjamini-Hochberg procedure, the process should involve calculating the probabilities and then rank these results in descending order in one operation, rather than doing separate tests by all births and birth order

• the Benjamini-Hochberg procedure may be supplemented with an analysis using Storey’s (2001) approach to estimate the local positive false discovery rate (pFDR)

• continue to aggregate 5 years of data in the analysis, to ensure that the sample size is adequate to be able to detect a specified difference

• in this analysis, DHSC uses a birth sex ratio of 107 males to 100 females. This is based on a review of available literature, advice from academic experts and on examination of data on birth sex ratios in more developed countries. ONS advised, that on this basis, one-sided tests against a ratio of 107 are appropriate

• previously, DHSC analysis has reported on male to female birth sex ratios for 2 or more children. However, as the birth order data for 2 or more children is closely related to 3 or more children, the recommendation was to no longer report the birth sex ratios for birth orders for 2 or more children

• there are a number of births where birth order is unknown. It is possible that any evidence of sex selection could show up in this category. Therefore, given that the birth order is of primary policy interest, the methodology review recommended reporting birth sex ratios and analyses for the unknown birth order from 2016

Further information

As part of the ongoing development of this publication, we are reviewing its content and methodology. If you have any feedback relating to this publication or are a user of these statistics and would like to be consulted about its content and/or methodology, get in touch at: [email protected]

Enquiries

Enquiries about the data or requests for further information should be addressed to:

Abortion Statistics Team
Department of Health and Social Care
10 South Colonnade
Canary Wharf
London
E14 4PZ

Email: [email protected]

Extracts from this publication may be reproduced provided a reference to the source is given.

Links

See all Sex ratios at birth: statistics.

See Abortion statistics 2021.

1. Hesketh, T and Xing, ZW (2006). Abnormal sex ratios in human populations: causes and consequences. Proceedings of the National Academy of Sciences, 103(36), 13271 to 13275 (viewed on 9 November 2022) ↩

2. Chahnazarian, A (1988). Determinants of the sex ratio at birth: review of recent literature. Social Biology, 35(3-4), 214 to 235 (viewed on 9 November 2022) ↩

3. Storey, JD (2002). A direct approach to false discovery rates. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(3), 479 to 498 (viewed on 9 November 2022) ↩

4. Storey, JD and Tibshirani, R (2003). Statistical significance for genomewide studies. Proceedings of the National Academy of Sciences, 100(16), 9440 to 9445 (viewed on 9 November 2022) ↩